While working on a game, I needed a data structure that could efficiently answer the question “do these two elements belong to the same set?”. I found the union-find data structure and it was exactly what I needed. I thought it was pretty cool so I decided to write about it.

Lets say you have a bunch of elements and you want to group them into sets. For example, you might have a bunch of people and you want to group them into families. You might have a bunch of numbers and you want to group them into ranges. Or you might have a bunch of points and you want to group them into clusters.

The union-find data structure is a clever system that keeps track of a partition of elements into disjoint (non-overlapping) sets, and allows you to efficiently answer the question “do these two elements belong to the same set?” or “who is the ultimate parent of this element?”. And path compression is a neat trick to make these operations even faster by remembering the result of previous find operations on the sets.

Lets continue our family example, lets say we are building a family tree tracking system where everyone in the family can be connected together by their ancestors. In this “family”, every person knows only their immediate parent but not necessarily their ultimate ancestor (or root).

The union-find data structure allows you to efficiently answer the question “do these two people belong to the same family?” or “who is the ultimate ancestor of this person?”.

This data structure supports two operations: “union” and “find”.

1. Union:

In this “family” example, the “union” operation means “Let’s unite two families”. When two people from two different families decide to get married, we perform a “union” operation to link these two families. We sometimes say one family “joins” the other.

2. Find:

The “find” operation is like asking, “Who’s the ultimate ancestor (or the root) of this person?”. This operation traces a person’s line of parents up to the ultimate ancestor.

Note: In a large family, it can take a long time to trace back up to the ultimate ancestor. To make this faster for next time, after we’ve found the ultimate ancestor of a person, we update that person’s immediate parent to be the ultimate ancestor (we “compress the path”). So next time we ask “who is this person’s ultimate ancestor?”, we get the answer in just one step.

Imagine you’re attending a huge family reunion. You meet a distant cousin and you both wonder how you’re related. So you both start asking your parents, who ask their parents, and so on, until you find the common ancestor. That’s a “find” operation. Now, to make it easier next time, you make a note that this cousin’s ultimate ancestor is the same as yours. That’s “path compression”.

By doing path compression, the union-find data structure ensures that the trees stay very flat, which makes future find operations much faster.

So in summary, the union-find data structure is a clever system that keeps track of a partition of elements into disjoint (non-overlapping) sets, and allows you to efficiently answer the question “do these two elements belong to the same set?” or “who is the ultimate parent of this element?”. And path compression is a neat trick to make these operations even faster by remembering the result of previous find operations.

Illustration

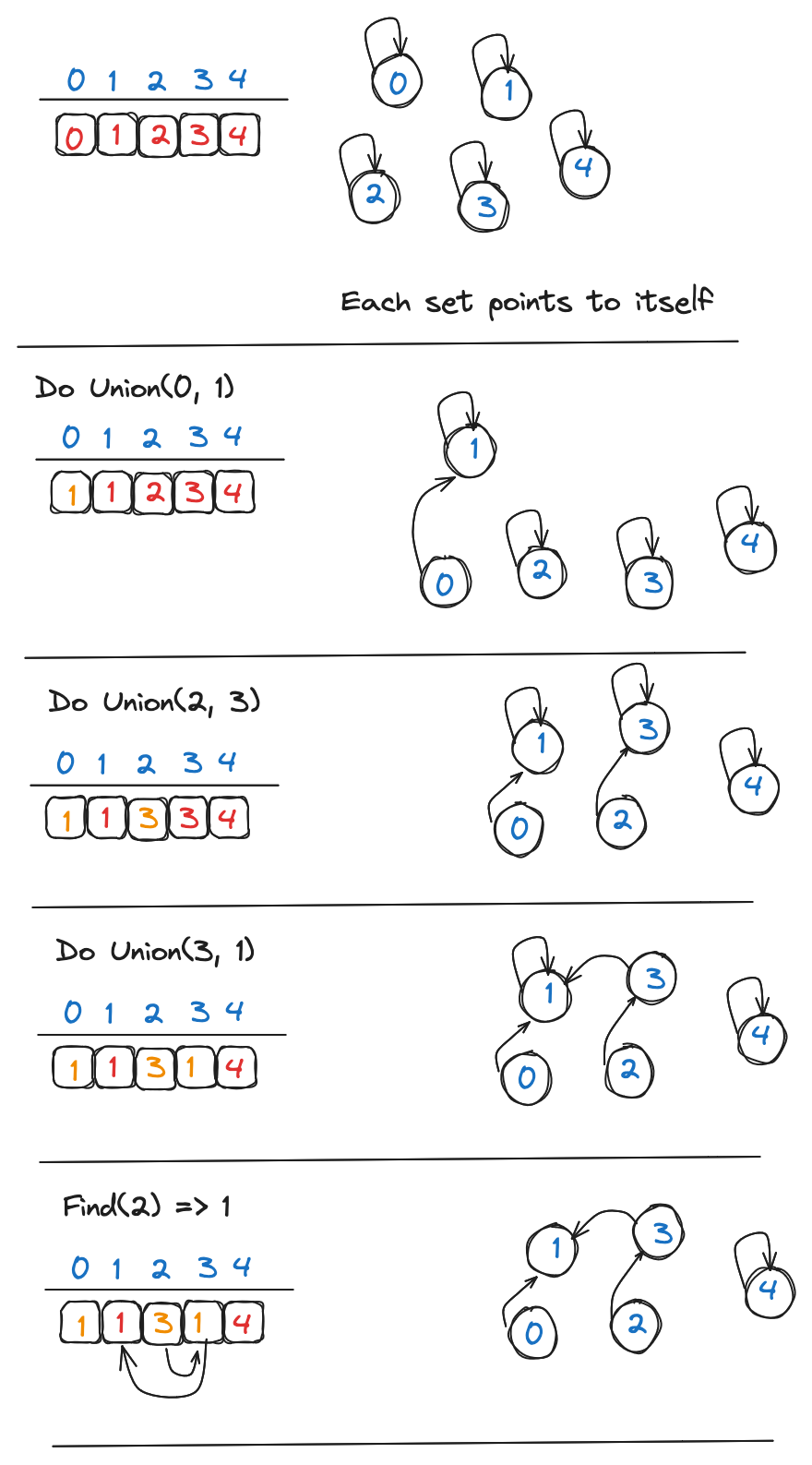
Implementation:

So this is how you would implement the union-find data structure in psuedocode:

1. Initialization

Start by initializing an array where the index represents each element and the value at each index represents the parent of that element. This is sometimes referred to as a “direct-access table” or a “lookup table.” For simplicity, let’s say we have 5 elements (0 to 4). At the start, each element is in a set by itself, so each element is its own parent.

          0, 1, 2, 3, 4
          -------------
parent = [0, 1, 2, 3, 4]

2. Find operation

The find operation will return the root of a given element (i.e., the representative of the set the element is in). This involves following the chain of parents until we find an element that is its own parent (i.e., parent[i] == i).

Here is a pseudocode function for find:

Function Find(a)
    while a != parent[a]
        a = parent[a]
    End While
    return a
End Function

For example, if we call Find(3), it will return 3. Thats pretty straightforward since 3 is its own parent :D.

3. Union operation

The union operation will connect or link two elements together. If we want to connect elements a and b, we need to find the root of a (which is the representative of the set a is currently in) and the root of b, and then set the parent of b’s root to be a’s root.

Here is a pseudocode function for union:

Function Union(a, b)
    aRoot = Find(a)
    bRoot = Find(b)
    parent[bRoot] = aRoot
End Function

For example, if we call Union(1, 3), the array becomes:

          0, 1, 2, 3, 4
          -------------
parent = [0, 1, 2, 1, 4]

Here, element 3’s parent is now 1, meaning elements 1 and 3 are in the same set.

4. Path Compression

We can optimize the find operation further with a technique called path compression. This involves making every node in the path from a to its root point directly to the root.

The find function with path compression would look like this:

Function Find(a)
    if a != parent[a]
        parent[a] = Find(parent[a])
    End If
    return parent[a]
End Function

This will “flatten” the tree over time, making subsequent find operations very fast.

And that’s it! Now you know how to implement a union-find data structure using an array. It’s a very useful and powerful data structure for solving problems that involve grouping elements into sets. I’ve implemented a version in go in case you want to play around with it.