The Kalman Filter

Behold a wiggly and smooth lines animation for effect :crowd-cheering:

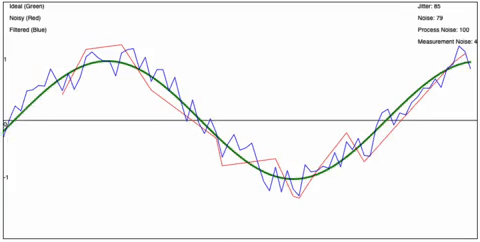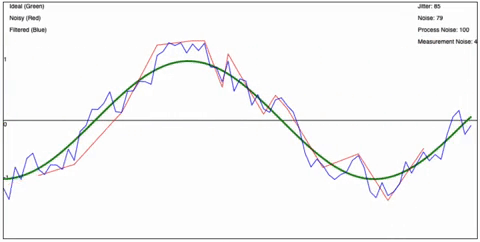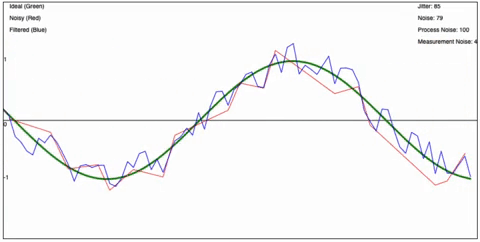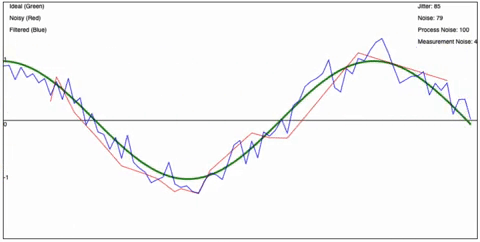
Its terrible example, but I got your attention now so lets go! <3

Intro

Imagine you’re in a virtual world, wearing a VR headset that tracks your movements so you can explore, fight dragons, or build castles. But oh no! The sensors inside your headset, called IMUs, can sometimes get a bit confused and think you’ve moved when you haven’t. This is called “drift,” and it can make you feel like you’re sliding or floating away in the game.

A Kalman Filter is an algorithm that helps correct their little mistakes and keeps track of where you really are, so you stay rooted in your virtual world. With a Kalman Filter, you can explore, battle, or build without worrying about drifting off course (bold claims to be verified, YMMV)! 🛡🐉🏰

Filter Steps Overview

This is how the kalman filter is described in the Wikipedia article:

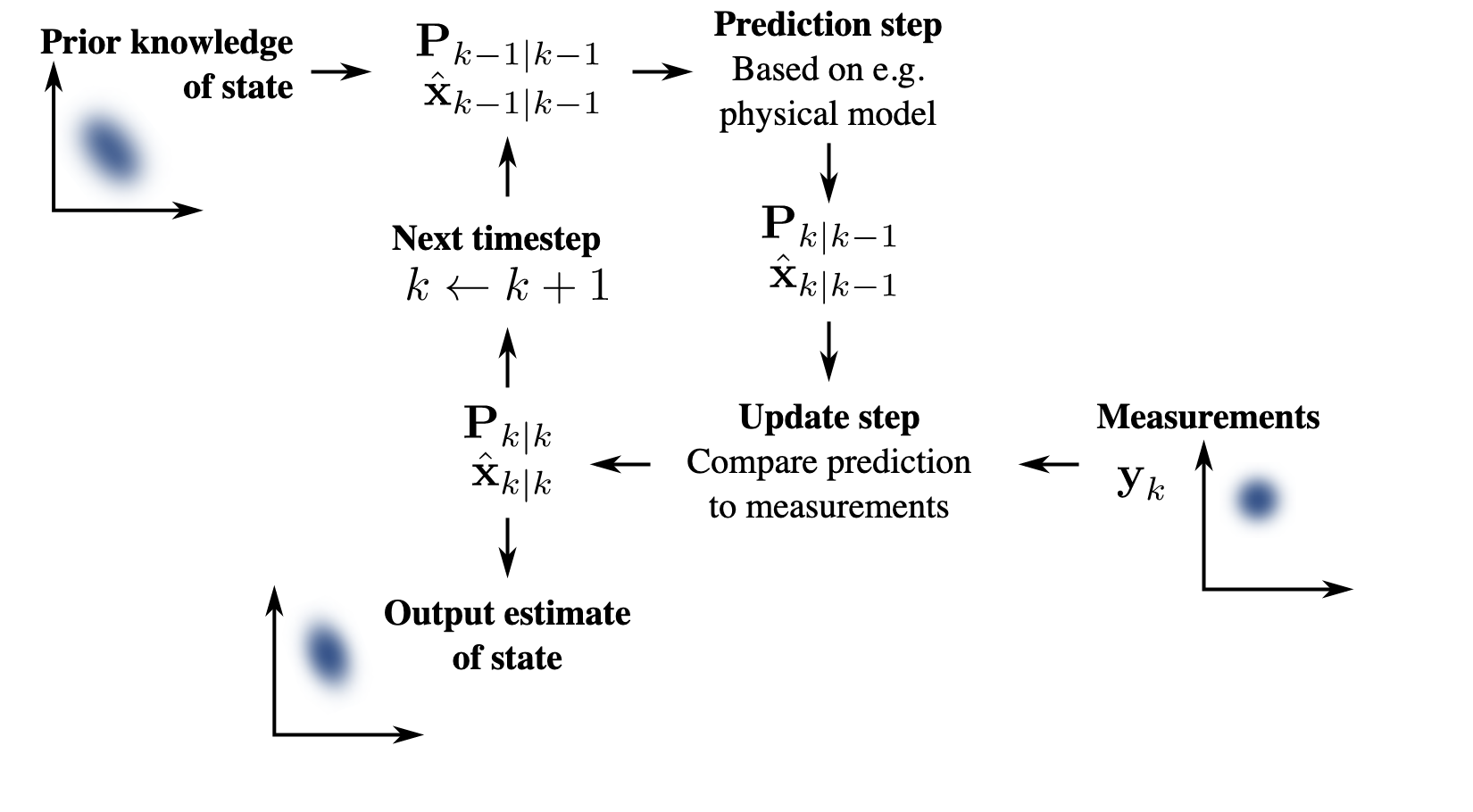
Its a bit scary, so I want to break it down into easier to digest steps that even I your humble author can understand (because I selfishly want to use it in another mad experiment).

Explanation of Each Part Of The Filter Process

Prediction

Before you get a new measurement, your “best guess” is what you already thought before. You just keep your old guess for now.

$$ Prediction=Previous Estimate $$

Update Estimation Error

Every time you make a new guess, it could be a little off. So, you add some “process noise” to say “my guess might wander a little each time.”

$$ Updated Error=Previous Error+Process Noise $$

Kalman Gain

Kalman Gain is like a “magic mixing number.” It decides how much to trust the new measurement compared to your prediction. If the measurement is really noisy, you’ll trust your prediction more, and vice versa.

$$ K=Updated ErrorUpdated Error+Measurement Noise $$

New Estimate

Now, you mix your prediction and the new measurement. You adjust your prediction based on how far off the measurement was. The amount you adjust is controlled by the Kalman Gain!

$$ New Estimate=Prediction+K×(Measurement−Prediction) $$

Thats it! Now you have a new estimate and how you sort of converge on values you can trust. You can use it for your next prediction, and the cycle continues.

A Key Insight Here: The Kalman Gain

The Kalman Gain is a value between 0 and 1 that determines how much to trust the measurement vs. the filters prediction. If the measurement is very noisy, the Kalman Gain will be close to 0, and the new estimate will be close to the previous estimate. If the measurement is very precise, the Kalman Gain will be close to 1, and the new estimate will be close to the measurement. Usually, the Kalman Gain is somewhere in between.

Essentially, it decides how much to trust new information from the sensor and how much to trust what we already know (the prediction).

And to represent it in a consise way:

$$ [ \text{Kalman Gain} = \frac{\text{Estimation Error}}{\text{Estimation Error} + \text{Measurement Noise}} ] ​ $$

Implementation In Code

Since the state needs to be kept since the last measurement, a class/object is very tidy fit for this problem because the state is tightly bound to the code. Let implement it now in JavaScript, its surprisingly easy and really just the steps outlined above.

The class needs to take the following parameters:

processNoise: This variable represents the expected noise or uncertainty in the process itself, separate from the measurements. In other words, even if you had a perfect measurement, the process you are measuring might naturally vary. For instance, if you’re measuring temperature, natural fluctuations occur even if your thermometer is perfect.

measurementNoise: This variable represents the expected noise or uncertainty in the measurements. It’s not about how the thing you’re measuring is changing; it’s about how imprecise your measurements are.

estimationError: This variable is your initial guess at how uncertain your initial estimate is. This is updated over time based on the measurements you take and whats called the Kalman Gain.

initialValue: This is your initial estimate of the value you’re tracking. For example, iif you’re tracking temperature and you have no idea what it is, you might start at a default like 0?

class KalmanFilter {
  constructor(
    processNoise,
    measurementNoise,
    estimationError,
    initialValue = 0
  ) {
    this.processNoise = processNoise;
    this.measurementNoise = measurementNoise;
    this.estimationError = estimationError;
    this.estimate = initialValue;
  }

  update(measurement) {
    // Step 1: Update estimation error based on process noise
    this.estimationError += this.processNoise;

    // Step 2: Calculate the Kalman Gain
    const kalmanGain =
      this.estimationError / (this.estimationError + this.measurementNoise);

    // Step 3: Update the current estimate
    this.estimate += kalmanGain * (measurement - this.estimate);

    // Step 4: Update the estimation error
    this.estimationError *= 1 - kalmanGain;

    // Return the updated estimate
    return this.estimate;
  }
}

Example Parameters For An IMU Kalman Filter:

initialValue: If you’re measuring orientation, a good initial value could be the angle given by the first sensor reading when you start the system. This assumes that you have a “boot-up” position that is relatively stable and known.

Why: Using the first measurement as an initial value is often a good idea because it’s usually the best estimate you have when starting the system right?!

estimationError: Since this is the beginning and you haven’t received much data yet, you could set this to a high value like 1.

Why: This high initial estimation error reflects your initial uncertainty about the orientation angle. It allows the filter to quickly adapt to the incoming measurements.

processNoise: Given the factors like temperature fluctuations, magnetic field variations, and potential for mechanical vibrations, a reasonable value might be 0.01.

Why: This value would allow for some inherent instability or drift in the IMU data but assumes that the sensor is reasonably reliable. You’re acknowledging that some error will accumulate over time but are optimistic it won’t be too bad.

measurementNoise: If you’re using a high-quality IMU with low sensor noise, a value like 0.05 might be appropriate.

Why: This value is lower than the processNoise because we assume that individual measurements are fairly accurate but not perfect. Lower measurementNoise compared to processNoise means you trust the measurements more than the internal state of the filter.

And in code it would look like this:

// Initialize the Kalman filter for the IMU
const imuKalmanFilter = new KalmanFilter(
  0.01,
  0.05,
  1 /* first sensor reading */
);

In Closing

And that, my friends is it. Its that simple. Now lets see it in action, I have created a page that shows the Kalman Filter in action using a little simulation that I wrote. You can play with the values and see how it affects the filter. The yellow line is the filtered signal, the red line is the “raw” IMU signal, and the white line is the “true” value – the perfect value if there was no noise or errors.

All of the code is also available, and you can remix it and play with it as you like https://glitch.com/edit/#!/kalman-filter-example?path=index.html

Until next time sweathearts! 💖